flowchart LR A>Mittelwertvergleich] --> B(unabhängige Stichprobe) B --> D(2 Faktorstufen) B --> E(mehr als 2 Faktorstufen) D --> F(t-test für unabhängige Stichprobe) D --> G(nicht parametrisch: Mann-Whitney Test) E --> H(Varianzanalyse: ein- und mehrfaktoriell) E --> I(nicht parametrisch: Kruskal-Wallis Test) A --> C(verbundene Stichprobe) C --> J(2 Faktorstufen) C --> K(mehr als 2 Faktorstufen) J --> L(t-test für verbundene Stichproben) J --> M(nicht parametrisch: Wilcoxon-Test) K --> N(einfaktorielle Varianzanalyse mit Messwiederholung) click I "https://patrickzerrer.github.io/R_Hands_on_Book/Skript_6.4.html#exkurs-nicht-parametrische-testverfahren" click H "https://patrickzerrer.github.io/R_Hands_on_Book/Skript_6.4.html" click N "https://patrickzerrer.github.io/R_Hands_on_Book/Skript_6.4.html#umgang-mit-messwiederholungen"
Bivariate Statistik & Mittelwertvergleiche

Bei der bivariaten Statistik schauen wir uns nicht Variablen isoliert an, sondern interessieren uns für die Beziehung von zwei Variablen zueinander. Grundsätzlich unterscheiden wir bei bivariaten Analysen in die Überprüfung von (Mittelwert-)Unterschieden und das Prüfen von Zusammenhängen. In diesem Kapitel konzentrieren wir uns auf die Überprüfung von Unterschieden. Die Überprüfung von Zusammenhängen mittels Korrelation und Regression findet sich hingegen im nächsten Kapitel.
1 Das Überprüfen von Unterschieden
Die Überprüfung von möglichen bivariaten Unterschieden sollte zunächst immer deskriptiv über Kreuztabellen oder Grafiken erfolgen.
Anschließend stehen uns eine Vielzahl an statistischen Testverfahren zur Verfügung. Diese nutzen wir um zu Überprüfen, ob ein eventueller Mittelwertunterschied in den deskriptiven Daten auch statistische Signifikanz aufweist.
Grundsätzlich unterscheiden wir zwischen Verfahren die eine verbundene Stichprobe und eine unabhängige Stichprobe voraussetzen. Bei einer unabhängigen Stichprobe sind unsere zu vergleichenden Gruppen unabhängig voneinander. Bei einer verbundenen Stichprobe hingegen hängen, wie es der Name schon vermuten lässt, die Stichproben voneinander ab. Ein klassisches Beispiel für eine verbundene Stichprobe ist der Mittelwertvergleich bei denselben Personen zu unterschiedlichen Zeitpunkten.
In einem nächsten Schritt schauen wir uns an, wie viele verschiedene Gruppen wir miteinander vergleichen. Vergleichen wir lediglich zwei Gruppen so nutzen wir einen t-test. Haben wir hingegen mehr als zwei Gruppen so können wir den t-test nicht mehr anwenden. Dann benötigen wir die Varianzanalyse.
In einem letzten Schritt müssen wir prüfen, ob unsere Daten für die Testverfahren geeignet sind. Sowohl der t-test als auch die Varianzanalyse stellen einige Voraussetzungen an die Beschaffenheit der Daten. Falls die Daten diese nicht erfüllen können wir auf weniger voraussetzungsreiche sog. nicht-parametrische Tests zurückgreifen.
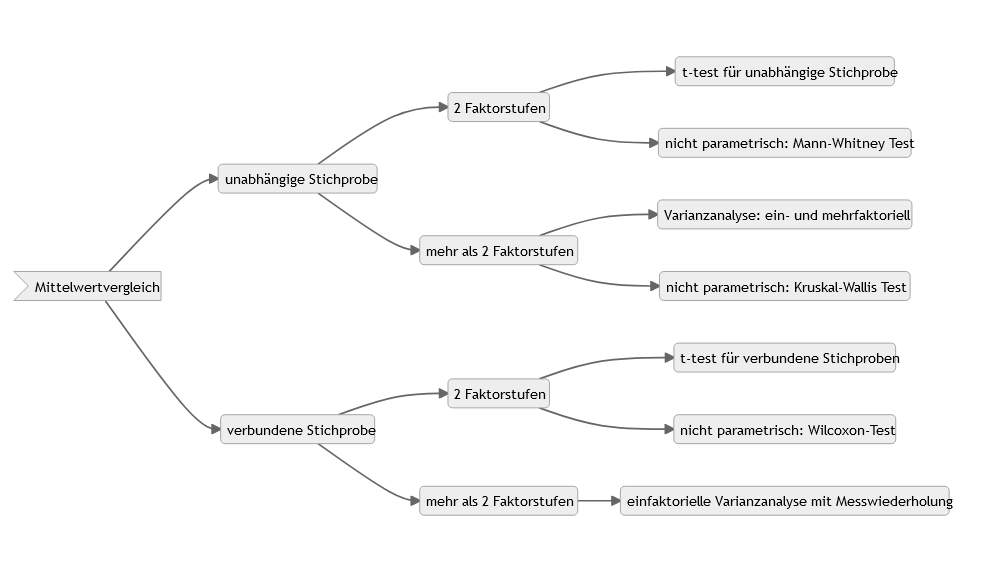
1.1 Wann verwende ich welches Testverfahren?
Die folgende Grafik kann als Orientierung dienen, welches Verfahren für eure spezielle Datenlage Sinn ergibt.