Die Faktorenanalyse

Author

Patrick Zerrer

Das Entdecken der zugrunde liegenden Struktur der Stadt, Bild generiert von Midjourney

Wir möchten - wie bereits in Kaptitel 5.1 angesprochen - ein Index für die von uns angenommene latente Variable Vertrauen in gesellschaftliche Institutionen bilden. An dieser Stelle müssten wir uns zunächst Gedanken über das Konstrukt Vertrauen in gesellschaftliche Institutionen machen und eine theoretische Grundlage entwickeln. Wir kürzen diesen Prozess an dieser Stelle etwas ab und möchten die lesende Person ermutigen einen kurzen Blick in den Aufsatz von Nina Steindl aus dem Jahr 2019 zum Vertrauen in gesellschaftliche Institutionen von Journalist:innen zu werfen. Wenn wir eine theoretische Vorstellung entwickelt haben, können wir mit der empirische Überprüfung der latenten Variable mittels explorativer Faktorenanalyse starten.

Die explorative Faktorenanalyse (EFA) ist eine statistischen Methoden, die dazu dient, die kleinste Anzahl hypothetischer Konstrukte (auch als Faktoren, Dimensionen, latente Variablen bezeichnet) zu ermitteln. Indem die beobachtete Kovarianz zwischen einer Reihe von Messvariablen (auch als beobachtete Variablen oder Indikatoren bezeichnet) erklärt wird. Konkret sollen die gemeinsamen Faktoren ermittelt werden, die die Struktur zwischen den gemessenen Variablen erklären. Wobei wir in den Sozialwissenschaften davon ausgehen, dass es sich bei diesen Faktoren um unbeobachtbare Merkmale - also latente Variablen - handelt.

Ein Faktor ist eine unbeobachtbare Variable, die mehr als eine beobachtete Messgröße beeinflusst und für die Korrelationen zwischen diesen beobachteten Messgrößen verantwortlich ist. Mit anderen Worten, die beobachteten Maße stehen in Beziehung zueinander, weil sie eine gemeinsame Ursache haben (d. h. sie werden von demselben zugrunde liegenden Konstrukt beeinflusst); wenn das latente Konstrukt abgetrennt wurde, sind die Interkorrelationen zwischen den beobachteten Maßen gleich Null. (Brown, 2015: 10)

In unserem Fall interessiert uns die latente Variable Vertrauen in gesellschaftliche Institutionen. Wir möchten Wissen, ob wir diese latente Variable bzw. diesen Faktor aus den einzelenen Indikatoren (den Fragen aus dem Allbus-Fragebogen) ableiten können. Konkret müssen wir überprüfen, ob sich die theoretisch angenommene latenten Variable auch in den Daten zu finden ist. Hierfür können wir die Faktorenanalyse oder Principal Component Analysis (PCA) verwenden.

Video

1 Data Management

Wir beginnen zunächst mit der Vorbereitung und Laden die notwendigen Pakete.

if(!require("pacman")) {install.packages("pacman");library(pacman)}
p_load(tidyverse, ggplot2, haven, psych, psy, nFactors, htmlTable)
theme_set(theme_classic())

1: Laden der Pakete mit p_load
2: Visualisierungshintergrund festlegen

Danach laden wir die Daten aus dem Allbus.

daten = haven::read_dta("Datensatz/Allbus_2021.dta")

1: Laden des Datensatzes

1.1 Auswahl der Variablen für die Faktorenanalyse

Die Variablen werden aufgrund ihrer Nützlichkeit als Indikatoren für die zu untersuchende latente Variable ausgewählt. Entsprechend ist es wichtig, dass die Variablen inhaltliche, diskriminante und konvergente Validität aufweisen. Etwas vereinfacht ausgedrückt sollten die Indikatoren über eine inhaltliche Passung zur latenten Variable verfügen, möglichst gut von anderen latenten Variablen abgrenzbar und mit mehreren unterschiedlichen Arten der Messung nachweisbar sein.

In unserem Fall möchten wir das Vertrauen in gesellschaftliche Institutionen untersuchen, entsprechend sollten wir Variablen bzw. Indikatoren auswählen, die die unterschiedlichen Bestandteile der latenten Variable abdecken.

Ganz konkret wählen wir Variablen aus, die das…

Vertrauen in das Gesundheitswesen (pt01)
Vertrauen in das Bundesverfassungsgericht (pt02)
Vertrauen in den Bundestag (pt03)
Vertrauen in die Stadt- oder Gemeindeverwaltung (pt04)
Vertrauen in die Katholische Kirche (pt06)
Vertrauen in die Evangelische Kirche (pt07)
Vertrauen in die Justiz (pt08)
Vertrauen in das Fernsehen (pt09)
Vertrauen in das Zeitungswesen (pt10)
Vertrauen in die Hochschulen (pt11)
Vertrauen in die Bundesregierung (pt12)
Vertrauen in die Polizei (pt14)
Vertrauen in die Politischen Parteien (pt15)
Vertrauen in die Kommission der EU (pt19)
Vertrauen in das Europäische Parlament (pt20)

… erfassen.

Für die statistische Identifizierung einer latenten Variablen bzw. eines Faktors werden mindestens drei gemessene Variablen benötigt, obwohl mehr Indikatoren vorzuziehen sind. Es werden beispielsweise auch vier bis sechs Indikatoren pro Faktor empfohlen. Im Allgemeinen funktioniert die EFA besser, wenn jeder Faktor überdeterminiert ist (d. h. es werden mehrere gemessene Variablen von der zu entdeckenden latenten Variable bzw. Faktor beeinflusst). Unabhängig von der Anzahl sollten Variablen, die voneinander abhängig sind, nicht in eine Faktorenanalyse einbezogen werden.

allbus_vertrauen = daten %>%
  select(pt01:pt20) %>%
  mutate(across(pt01:pt20, ~ as.numeric(.))) %>%
  mutate(across(pt01:pt20, ~ ifelse(.%in% c(-9, -11, -42), NA,.))) %>%
  na.omit()

1: Wir erstellen ein neues Objekt basierend auf dem Datensatz daten
2: Mit dem Doppelpunkt wählen wir alle Variablen zwischen pt01 bis pt20 aus
3: Die Kombination aus mutate und across ermöglicht es uns die Funktion as.numeric in einer Zeile auf alle zuvor ausgewählten Variablen anzuwenden. Die ~ gibt den Start der anzuwenden Funktion (hier as.numeric an), der Punkt innerhalb der Klammer der as.numeric Funktion dient als eine Art Platzhalter für die zuvor ausgewählten Variablen
4: Wir codieren die unterschiedlichen fehlenden Werte um (aus der Allbus-Dokumentation entnommen). Hierfür greifen wir auf die Funktion if_elsezurück. Dabei handelt es sich um ein Entweder-Oder-Befehl. Konkret wird zunächst eine Bedingung geprüft und dann auf dieser Grundlage entweder Option 1 oder Option 2 ausgeführt. Der Punkt vor %in% dient wiederum als Platzhalter, mit dem Ausdruck %in% prüfen wir, ob die nachfolgenden Werte (also c(-9, -11, -42)) in der jeweiligen Variable vorkommen. Hierbei handelt es sich um unsere Bedingung für den Entweder-Oder-Befehl. Wenn einer der Werte aus der geprüften Variable einem der spezifizierten Werte entspricht - also unsere Bedingung erfüllt - wird dieser durch NA ersetzt. Ist die Bedingung nicht erfüllt, wird die andere Option ausgeführt und der bereits existierende Wert wird beibehalten.
5: Wir entfernen mit der Funktion na.omit fehlende Werte aus dem Datensatz

Wir bennen die ausgewählten Indikatoren um, damit die Bezeichnungen der Indikatoren für uns leichter zu merken sind.

allbus_vertrauen = allbus_vertrauen %>% 
  
  rename(Ver_Gesundheitswesen = pt01,
         Ver_BVerfG = pt02,
         Ver_Bundestag = pt03,
         Ver_Verwaltung = pt04,
         Ver_kath_Kirche = pt06,
         Ver_evan_Kirche = pt07,
         Ver_Justiz = pt08,
         Ver_TV = pt09,
         Ver_Zeitung = pt10,
         Ver_Uni = pt11,
         Ver_Regierung = pt12,
         Ver_Polizei = pt14,
         Ver_Parteien = pt15,
         Ver_Kom_EU = pt19,
         Ver_EU_Par = pt20)

htmlTable(head(allbus_vertrauen))

1: Mit dem rename Befehl können wir die Variablen umbennen
2: Wir überprüfen kurz, ob die Umbenennung geklappt hat und lassen uns die ersten Zeilen des Datensatzes anzeigen. Hierfür nutzen wir htmlTable für eine schönere Darstellung der Tabelle sowie head, um uns die ersten paar Zeilen des Datensatzes allbus_vertrauen anzeigen zu lassen

	Ver_Gesundheitswesen	Ver_BVerfG	Ver_Bundestag	Ver_Verwaltung	Ver_kath_Kirche	Ver_evan_Kirche	Ver_Justiz	Ver_TV	Ver_Zeitung	Ver_Uni	Ver_Regierung	Ver_Polizei	Ver_Parteien	Ver_Kom_EU	Ver_EU_Par
1	7	7	4	2	3	7	4	2	4	7	6	3	3	5	5
2	4	7	4	4	2	5	5	5	5	5	6	5	4	5	6
3	3	4	5	6	1	3	6	4	4	4	5	6	4	4	4
4	5	5	4	5	3	5	4	5	6	6	4	5	3	5	5
5	4	7	5	3	2	2	5	3	4	5	5	6	3	3	3
6	3	3	3	3	1	2	3	3	3	4	4	4	2	2	2

Neben der Auswahl der Variablen bzw. Indikatoren müssen auch die Fälle (in unserem Fall die Anzahl der befragten Personen) festgelegt werden. Hier sollten wir uns zunächst fragen, ob die Stichprobe der Teilnehmer:innen in Bezug auf die gemessenen Indikatoren sinnvoll ist? Handelt es sich um eine repräsentative Stichprobe? Bei dem Allbus ist das der Fall und entsprechend können wir davon ausgehen, dass wir eine passende Stichprobe für die Durchführung eine Faktorenanalyse vorliegen haben.

2 Deskriptive Statistik für den Teildatensatz

Wir werfen einen kurzen Blick in die deskriptive Statistik für unseren Teildatensatz, um ein besseres Verständnis für die Daten zu erhalten.

summary(allbus_vertrauen)

1: Mit dem summary Befehl können wir uns die deskritpive Statistik ausgeben lassen

 Ver_Gesundheitswesen   Ver_BVerfG    Ver_Bundestag   Ver_Verwaltung 
 Min.   :1.000        Min.   :1.000   Min.   :1.000   Min.   :1.000  
 1st Qu.:4.000        1st Qu.:4.000   1st Qu.:3.000   1st Qu.:4.000  
 Median :5.000        Median :6.000   Median :4.000   Median :5.000  
 Mean   :4.939        Mean   :5.255   Mean   :4.058   Mean   :4.482  
 3rd Qu.:6.000        3rd Qu.:6.000   3rd Qu.:5.000   3rd Qu.:5.000  
 Max.   :7.000        Max.   :7.000   Max.   :7.000   Max.   :7.000  
 Ver_kath_Kirche Ver_evan_Kirche   Ver_Justiz        Ver_TV     
 Min.   :1.000   Min.   :1.00    Min.   :1.000   Min.   :1.000  
 1st Qu.:1.000   1st Qu.:1.00    1st Qu.:4.000   1st Qu.:3.000  
 Median :2.000   Median :3.00    Median :5.000   Median :4.000  
 Mean   :2.331   Mean   :3.04    Mean   :4.581   Mean   :3.577  
 3rd Qu.:3.000   3rd Qu.:4.00    3rd Qu.:6.000   3rd Qu.:4.000  
 Max.   :7.000   Max.   :7.00    Max.   :7.000   Max.   :7.000  
  Ver_Zeitung       Ver_Uni      Ver_Regierung    Ver_Polizei     Ver_Parteien 
 Min.   :1.000   Min.   :1.000   Min.   :1.000   Min.   :1.000   Min.   :1.00  
 1st Qu.:3.000   1st Qu.:4.000   1st Qu.:3.000   1st Qu.:4.000   1st Qu.:2.00  
 Median :4.000   Median :5.000   Median :4.000   Median :5.000   Median :3.00  
 Mean   :4.012   Mean   :5.203   Mean   :4.054   Mean   :4.948   Mean   :3.19  
 3rd Qu.:5.000   3rd Qu.:6.000   3rd Qu.:5.000   3rd Qu.:6.000   3rd Qu.:4.00  
 Max.   :7.000   Max.   :7.000   Max.   :7.000   Max.   :7.000   Max.   :7.00  
   Ver_Kom_EU      Ver_EU_Par   
 Min.   :1.000   Min.   :1.000  
 1st Qu.:2.000   1st Qu.:2.000  
 Median :4.000   Median :4.000  
 Mean   :3.515   Mean   :3.556  
 3rd Qu.:5.000   3rd Qu.:5.000  
 Max.   :7.000   Max.   :7.000

3 Prüfung der Vorraussetzungen der Faktorenanalyse

Die Faktorenanalyse bringt, wie jedes statistische Verfahren, eine Reihe von Vorraussetzungen mit.

Diese sind: - Varianz - Linearität - Normalverteilung - Level der Messung - Fehlende Werte - Ausreißer - Korrelation der Variablen untereinander

Diese Vorraussetzungen sollten wir kennen und bei der Anwendung der Faktorenanalyse beachten. Viele der Vorraussetzungen beziehen sich auf Pearson-Korrelationskoeffizienten, welcher die statistsiche Grundlage für die Berechnung der Faktoren bildet.

3.1 Varianz

Wir sollten sichergehen, dass die Daten aus unserer Stichprobe ausreichend varrieren. Wir werfen hierfür ein Blick in die Daten.

colors = c(rep("darkgreen", 1))

ggplot(allbus_vertrauen, aes(x = Ver_Gesundheitswesen)) +
  geom_histogram(binwidth = 0.5, fill = colors)

1: Visuelle Überprüfung mit einem Histogram für die erste Variable Ver_Gesundheitswesen. Die restlichen Variablen sollten auch überprüft werden.

3.2 Linearität

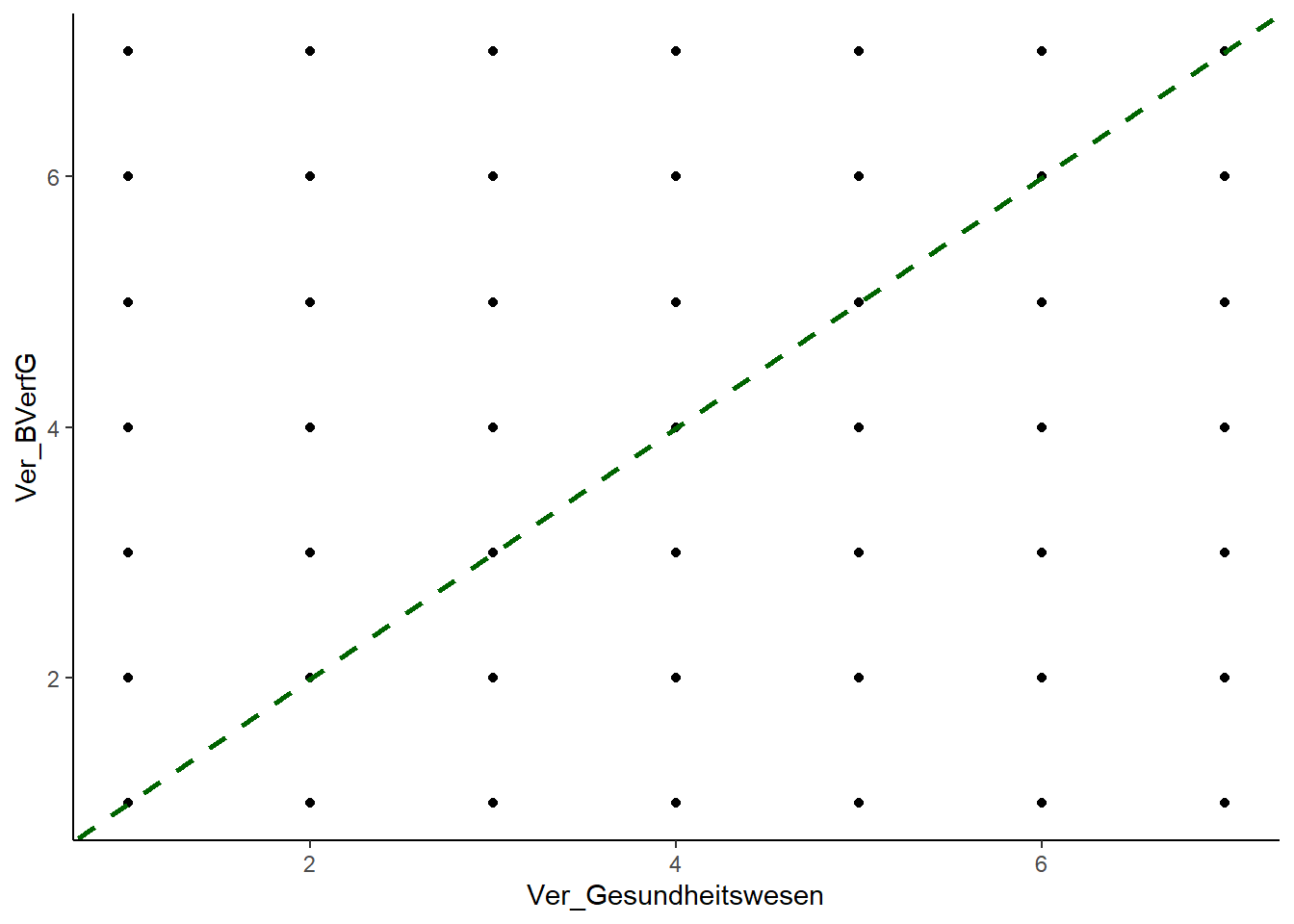
Der Pearson-Korrelationskoeffizient (r) misst die lineare Beziehung zwischen zwei Variablen. Wenn die tatsächliche Beziehung nicht linear ist, dann verringert sich der Wert von r. Wir können auf Linearität u.a. visuell durch das Betrachten der Daten mittel Streudiagramm prüfen.

ggplot(allbus_vertrauen, aes(x = Ver_Gesundheitswesen, y = Ver_BVerfG)) +
  geom_point() +
  geom_abline(linetype = "dashed", color = "darkgreen", size = 1)

1: Visuelle Überprüfung mit einem Streudiagramm für die erste Variable Ver_Gesundheitswesen & Ver_BVerfG. Die restlichen Variablen sollten auch überprüft werden.

3.3 Normalverteilung

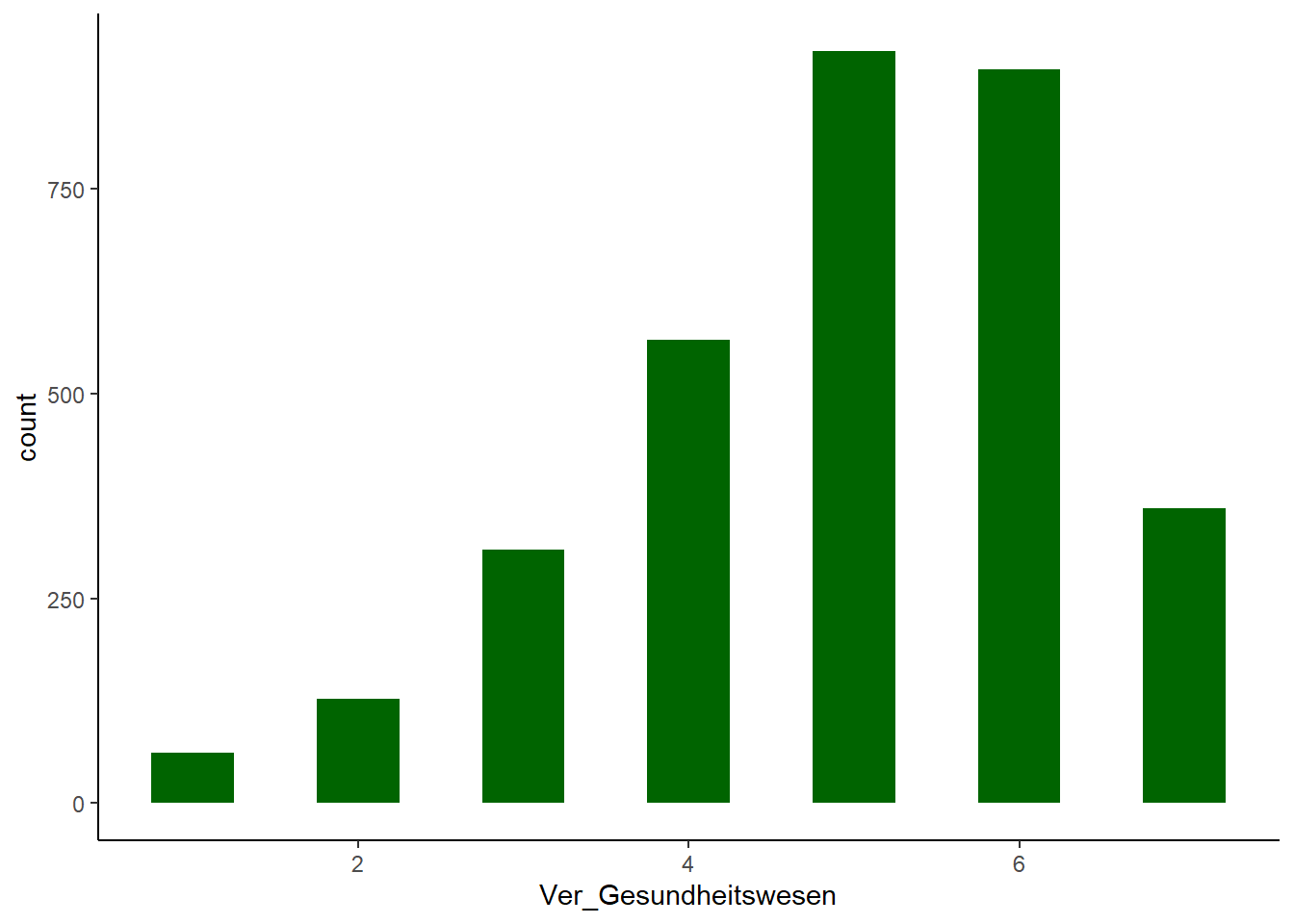
Der Pearson-Korrelationskoeffizient setzt eine Normalverteilung voraus. Allerdings finden sich in der Realität fast nie perfekt normalverteilte Daten. Schiefe und Kurtosis sind besonders einflussreich die Ergebnisse der Faktorenanalyse und können im Extremfall artefaktische Ergenbnisse erzeugen.

colors = c(rep("darkgreen", 1))

ggplot(allbus_vertrauen, aes(x = Ver_Gesundheitswesen)) +
  geom_histogram(binwidth = 0.5, fill = colors)

2: Statistische Überprüfung mittels Shapiro Wilk Test für die erste Variable Ver_Gesundheitswesen. Ein p-Wert unter 0.05 = keine Normalverteilung und ein p-Wert über 0.05 = Normalverteilung

shapiro.test(allbus_vertrauen$Ver_Gesundheitswesen)


    Shapiro-Wilk normality test

data:  allbus_vertrauen$Ver_Gesundheitswesen
W = 0.92081, p-value < 2.2e-16

3.4 Messniveau der Variablen

Bei Pearson-Korrelationen wird davon ausgegangen, dass normalverteilte Variablen auf Intervall- oder Verhältnisskalen gemessen werden, d. h. es handelt sich um kontinuierliche Daten mit gleichen Intervallen. Diese Eigenschaften treffen nicht auf ordinale (bspw. Kategorien) oder dochotome (bspw. Wahr-Falsch-Items) Variablen zu, was sich negativ auf Pearson-Korrelationskoeffizieten auswirkt und zu verzerrten Ergebnissen führen kann. Allerdings ist ein beträchtlicher Teil der Daten, mit denen wir zu tun haben, ordinal oder dichotom skaliert, um auch mit diesen Daten arbeiten zu können nutzen wir die polychorische Korrelation, welche robuster Nicht-Normalverteilung ist.

3.5 Fehlende Werte

In jeder Studie sollten wir die Anzahl und die Art der fehlenden Werte sowie die Gründe und die Methoden für den Umgang mit diesen Daten angegeben werden.

allbus_vertrauen = allbus_vertrauen %>%   
  mutate(across(Ver_Gesundheitswesen:Ver_EU_Par, ~ ifelse(.%in% c(-9, -11, -42), NA,.))) %>%
  na.omit()

1: Wir codieren die unterschiedlichen fehlenden Werte um (aus der Allbus-Dokumentation entnommen). Hierfür greifen wir auf die Funktion if_elsezurück. Dabei handelt es sich um ein Entweder-Oder-Befehl. Konkret wird zunächst eine Bedingung geprüft und dann auf dieser Grundlage entweder Option 1 oder Option 2 ausgeführt. Der Punkt vor %in% dient wiederum als Platzhalter. Während %in% angibt, ob die nachfolgenden Werte (also c(-9, -11, -42)) in der jeweiligen Variable vorkommen. Hierbei handelt es sich um unsere Bedingung für den Entweder-Oder-Befehl. Wenn einer der Werte aus der geprüften Variable einem der spezifizierten Werte entspricht - also unsere Bedingung erfüllt - wird dieser durch NA ersetzt. Ist die Bedingung nicht erfüllt, wird die andere Option ausgeführt und der bereits existierende Wert wird beibehalten.
2: Wir entfernen mit der Funktion na.omit fehlende Werte aus dem Datensatz

3.6 Ausreißer

Wir sollten Ausreißer identifizieren und im Zweifel von der Analyse ausschließen, da diese zu einer Verzerrung der Ergebnisse führen können. Zu den Methoden zur Erkennung von Ausreißern gehören Boxplots und Streudiagramme für einzelne Variablen sowie der Mahalanobis-Abstand für mehrere Variablen.

boxplot(allbus_vertrauen)

1: Erstellen des Boxpltos

3.7 Korrelation der Variablen untereinander

Wir sollten trotz unserer guten Datengrundlage nochmals prüfen, ob die gemessenen Variablen ausreichend miteinander korreliert sind, um eine Faktorenanalyse zu rechtfertigen. Eine Korrelation zwischen zwei Variablen gibt an, ob und wie stark ein Zusammenhang zwischen den beiden Variablen besteht. An dieser Stelle ist es wichtig, sich zu merken, dass eine Korrelation die Stärke eines Zusammenhangs angibt. Eine genauere Erklärung findet ihr im Kapitel 7. Zunächst können wir einen Blick in die Korrelationsmatrix werfen - eine beträchtliche Anzahl von Korrelationen sollte ±.30 überschreiten. Alternativ können wir ein objektiveren Test der Faktorfähigkeit der Korrelationsmatrix durchführen. Hierfür greifen wir auf den Sphärizitätstest nach Bartlett (1954) zurück.

htmlTable(round(cor(allbus_vertrauen), digits = 3))

1: Die htmlTable Funktion ermöglicht uns eine schönere Darstellung der Tabelle, round rundet die Werte auf die von uns mit digits = 3 festgelegten drei Nachkommastellen, während wir mit cor die Korrelationen für die Werte in unserem Datensatz allbus_vertrauen berechnen

	Ver_Gesundheitswesen	Ver_BVerfG	Ver_Bundestag	Ver_Verwaltung	Ver_kath_Kirche	Ver_evan_Kirche	Ver_Justiz	Ver_TV	Ver_Zeitung	Ver_Uni	Ver_Regierung	Ver_Polizei	Ver_Parteien	Ver_Kom_EU	Ver_EU_Par
Ver_Gesundheitswesen	1	0.435	0.446	0.375	0.184	0.21	0.384	0.337	0.334	0.37	0.43	0.413	0.349	0.359	0.357
Ver_BVerfG	0.435	1	0.629	0.397	0.148	0.223	0.635	0.385	0.424	0.474	0.561	0.45	0.429	0.456	0.476
Ver_Bundestag	0.446	0.629	1	0.553	0.267	0.323	0.571	0.483	0.487	0.42	0.816	0.445	0.677	0.656	0.661
Ver_Verwaltung	0.375	0.397	0.553	1	0.274	0.306	0.471	0.361	0.377	0.384	0.485	0.422	0.472	0.456	0.455
Ver_kath_Kirche	0.184	0.148	0.267	0.274	1	0.699	0.23	0.2	0.202	0.138	0.261	0.219	0.301	0.288	0.284
Ver_evan_Kirche	0.21	0.223	0.323	0.306	0.699	1	0.271	0.258	0.279	0.2	0.327	0.27	0.35	0.328	0.325
Ver_Justiz	0.384	0.635	0.571	0.471	0.23	0.271	1	0.356	0.418	0.453	0.56	0.53	0.48	0.534	0.541
Ver_TV	0.337	0.385	0.483	0.361	0.2	0.258	0.356	1	0.714	0.378	0.49	0.351	0.492	0.411	0.415
Ver_Zeitung	0.334	0.424	0.487	0.377	0.202	0.279	0.418	0.714	1	0.488	0.502	0.365	0.489	0.456	0.461
Ver_Uni	0.37	0.474	0.42	0.384	0.138	0.2	0.453	0.378	0.488	1	0.467	0.409	0.368	0.43	0.435
Ver_Regierung	0.43	0.561	0.816	0.485	0.261	0.327	0.56	0.49	0.502	0.467	1	0.494	0.719	0.699	0.694
Ver_Polizei	0.413	0.45	0.445	0.422	0.219	0.27	0.53	0.351	0.365	0.409	0.494	1	0.414	0.374	0.37
Ver_Parteien	0.349	0.429	0.677	0.472	0.301	0.35	0.48	0.492	0.489	0.368	0.719	0.414	1	0.707	0.696
Ver_Kom_EU	0.359	0.456	0.656	0.456	0.288	0.328	0.534	0.411	0.456	0.43	0.699	0.374	0.707	1	0.957
Ver_EU_Par	0.357	0.476	0.661	0.455	0.284	0.325	0.541	0.415	0.461	0.435	0.694	0.37	0.696	0.957	1

Noch zu prüfen ist die Korrelation der Items miteinander, hierfür nehmen wir den Bartlett Test.

cortest.bartlett(allbus_vertrauen)

1: Wir führen den Bartlett-Test durch

$chisq
[1] 33164.76

$p.value
[1] 0

$df
[1] 105

Bei großen Stichprobenumfängen, wie in unserem Fall mit dem Allbus, reagiert der Bartlett-Test selbst auf geringfügige Abweichungen vom Zufallsprinzip empfindlich, so dass seine Ergebnisse durch ein Maß für die Stichprobenadäquanz ergänzt werden sollten. Das Kaiser-Meyer-Olkin (KMO; Kaiser, 1974) Maß für die Stichprobenadäquanz ist das Verhältnis von Korrelationen und partiellen Korrelationen, das das Ausmaß widerspiegelt, in dem Korrelationen eine Folge der über alle Variablen geteilten Varianz sind und nicht der von bestimmten Variablenpaaren geteilten Varianz.

KMO(allbus_vertrauen)

1: Wir lassen uns das KMO berechnen

Kaiser-Meyer-Olkin factor adequacy
Call: KMO(r = allbus_vertrauen)
Overall MSA =  0.89
MSA for each item = 
Ver_Gesundheitswesen           Ver_BVerfG        Ver_Bundestag 
                0.96                 0.91                 0.91 
      Ver_Verwaltung      Ver_kath_Kirche      Ver_evan_Kirche 
                0.95                 0.73                 0.78 
          Ver_Justiz               Ver_TV          Ver_Zeitung 
                0.94                 0.87                 0.88 
             Ver_Uni        Ver_Regierung          Ver_Polizei 
                0.94                 0.92                 0.94 
        Ver_Parteien           Ver_Kom_EU           Ver_EU_Par 
                0.97                 0.83                 0.83

KMO-Werte reichen von 0,00 bis 1,00 und können sowohl für die gesamte Korrelationsmatrix als auch für jede gemessene Variable berechnet werden. Insgesamt sind KMO-Werte ≥.70 erwünscht und Werte unter .50 werden im Allgemeinen als inakzeptabel angesehen. In diesem Fall ist die Korrelationsmatrix nicht faktoriell.

4 Durchführung der Faktorenanalyse

Wenn wir den Begriff Faktorenanalyse verwenden, meinen wir meistens zwei eigentlich unterschiedliche Verfahren, die sich in Zweck und Berechnung unterscheiden: die Hauptkomponentenanalyse (PCA) und die explorative Faktorenanalyse. Die Hauptkomponentenanalyse analysiert die gesamte Korrelationsmatrix und zielt darauf ab, Daten zu reduzieren und dabei so viele Informationen aus dem ursprünglichen Datensatz wie möglich zu erhalten. Zu diesem Zweck berechnet die Hauptkomponentenanalyse sogenannte Linearkombinationen der ursprünglichen Messvariablen, die so viele Informationen wie möglich erklären. Diese neuen Messvariablen werden als sogenannte Komponenten bezeichnet und sind im engeren Sinn keine latenten Konstrukte.

Die Faktorenanalyse versucht im Unterschied dazu, die Gesamtvarianz der gemessenen Variablen in gemeinsame Varianz (Kommmunialität oder h2) und die einzigartige Varianzen (u2) zu trennen. Dies geschieht indem eine reduzierte Korrelationsmatrix analysiert wird, bei der eine Schätzung der gemeinsamen Varianz jeder Messvariablen auf der Diagonalen der Korrelationsmatrix platziert wird.

Zusammenfassend liefern beide Methoden, also sowohl die PCA als auch die Faktorenanalyse eine Schätzungen der Gemeinsamkeit, aber nur die Faktorenanalyse kann die Einzigartigkeit (u2) jeder gemessenen Variable schätzen.

Die meisten Methodiker:innen empfehlen, dass die explorative Faktorenanalyse für eine Theoriebildung verwendet wird, um latente Konstrukte zu identifizieren. Fabrigar und Wegener (2012) empfahlen zum Beispiel Folgendes:

When the goal of research is to identify latent constructs for theory building or to create measurement instruments in which the researcher wishes to make the case that the resulting measurement instrument reflects a meaningful underlying construct, we argue that common factor analysis (EFA) procedures are usually preferable. (Fabrigar und Wegener, 2012: 32)

In unserem Fall wenden wir eine konfirmatorische Faktorenanalyse (PCA) an, da wir uns für die latente Variable Vertrauen in gesellschaftliche Institutionen interessieren und hierfür bereits eine theoretischer Rahmen besteht. Hierfür greifen wir auf das psych-Paket zurück, welches die Funktion principal für eine Faktorenanalyse enthält.

4.1 Methode der Schätzung

Nachdem wir die Faktorenanalyse (EFA) als bevorzugtes Modell festgelegt haben, müssen wir noch die Methode zur Schätzung (Extraktion) des Faktorenmodells auswählen. Konkret suchen wir ein mathematischen Verfahren, dass die Beziehungen zwischen den gemessenen Variablen und den Faktoren (d. h. die Regression der gemessenen Variablen auf die gemeinsamen Faktoren) möglichst genau schätzt.

Wir möchten kurz anmerken, dass der mathematische Hintergrund an dieser Stelle des Kurses noch nicht so wichtig ist, da hier einige Grundlagen erst imd Kapitel 7 erklärt werden. Trotzdem macht es unserer Einschätzung nach Sinn die Begriffe bereits zu kennen und deren Vor- und Nachteile bennen zu können.

Es existieren eine ganze Reihe von unterschiedlichen Schätzmethoden, von denen zwei Methoden am häufigsten angewendet werden. (1) Die ML-Schätzung (Maximum Liklelihood) beruht auf der Normalverteilung und ist entsprechend empfindlicher multivariater Normalität und erfordert meistens einen größere Stichprobe (mehr Fälle). (2) Die PA (wird auch als Hauptfaktoren, MINRES oder OLS bezeichnet) ist im Gegenzug dazu eine Methode der kleinsten Quadrate, welche keine Annahmen über Verteilungen trifft. PA nutzt hier eine wiederholte Zwischenschätzung, welche eine bessere Schätzung der Gemeinsamkeit ermöglicht und wiederholt diese bis eine zufriedenstellende Lösung erreicht ist.

Die PA eignet sich als Methode der Schätzung insbesondere dann, wenn der Zusammenhang zwischen den gemessenen Variablen und den Faktoren relativ schwach sind (≤.40), der Stichprobenumfang relativ klein ist (≤300), die multivariate Normalität verletzt ist oder wenn die Anzahl der den gemessenen Variablen zugrunde liegenden Faktoren falsch spezifiziert ist. Im Gegensatz dazu ist eine ML-Schätzung besser geeignet, wenn die Beziehungen zwischen Faktoren und Variablen stark sind (>.40), der Stichprobenumfang groß ist, multivariate Normalität erreicht wird und die Anzahl der Faktoren korrekt angegeben ist.

Wir können für unser Beispiel weiterhin die Maximum-likelihood Faktorenanalyse aus dem psych-Paket mit der Funktion principal verwenden, da wir in unserem Fall die entsprechenden Voraussetzungen in Bezug auf den Stichprobenumfang, die Stärke der Beziehung, sowie der Anzahl der Faktoren erfüllen. Für dieses Beispiel nutzen wir trotz der nicht perfekten Normalverteilung die ML Methode, alternativ könnten die PA Methode als robustere Variante nehmen.

4.2 Anzahl der Faktoren

Wie bereits bei der ML-Schätzung angedeutet, müssen wir die Anzahl der Faktoren festlegen. Hierfür müssen wir die Anzahl der Faktoren für die weitere Analyse festlegen. Wir erreichen das indem wir mehrere Modelle schätzen und somit Rückschlüsse auf ein optimales Modell mit der für uns passenden Anzahl an Faktoren ziehen. Vereinfacht können wir uns das Auswringen eines nassen Handtuchs vorstellen, bei der der erste Faktor die meiste Varianz extrahiert - ergo die größte Mene an Wasser - und die nachfolgenden Faktoren sukzessive kleinere Anteile der Varianz extrahieren. Auf diese Art und Weise können wir eine Schätzung des optimalen Modells vornehmen.

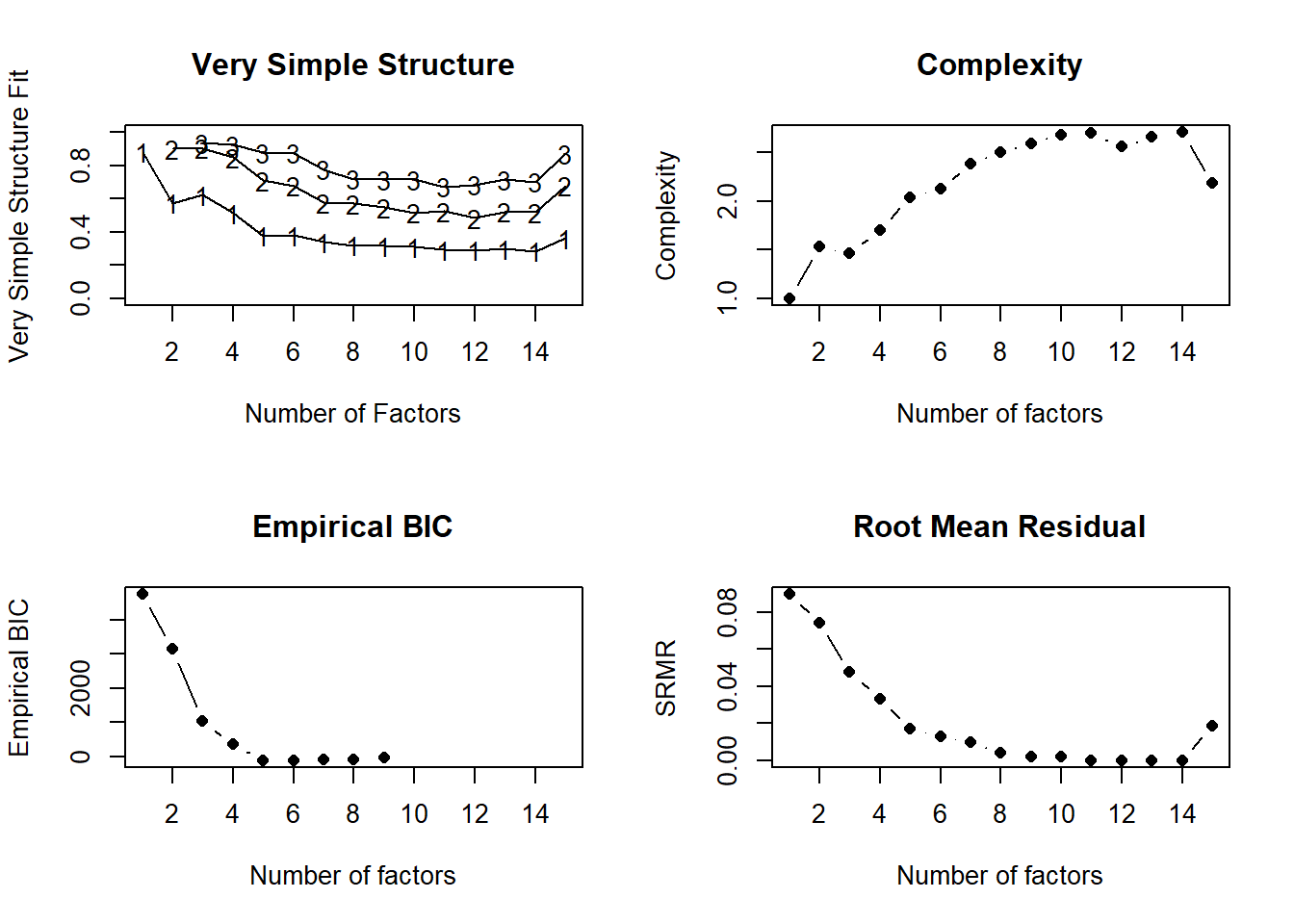
Wir verwenden hierfür die nfactors-Funktion, welche uns mehere Schätzungen ausgibt.

nfactors(allbus_vertrauen, rotate = "varimax", fm="mle")

1: Mit der nfactors Funktion können wir verschiedene Schätzungen durchführen. Hierfür wählen wir ein Rotation mit rotate aus, sowie eine Methode der Schätzung mittels fm


Number of factors
Call: vss(x = x, n = n, rotate = rotate, diagonal = diagonal, fm = fm, 
    n.obs = n.obs, plot = FALSE, title = title, use = use, cor = cor)
VSS complexity 1 achieves a maximimum of 0.88  with  1  factors
VSS complexity 2 achieves a maximimum of 0.9  with  3  factors
The Velicer MAP achieves a minimum of 0.04  with  1  factors 
Empirical BIC achieves a minimum of  -125.8  with  6  factors
Sample Size adjusted BIC achieves a minimum of  -26  with  8  factors

Statistics by number of factors 
   vss1 vss2   map dof   chisq     prob sqresid  fit RMSEA  BIC SABIC complex
1  0.88 0.00 0.035  90 1.0e+04  0.0e+00     7.0 0.88 0.187 9520  9806     1.0
2  0.57 0.90 0.040  76 5.0e+03  0.0e+00     5.8 0.90 0.141 4348  4590     1.5
3  0.62 0.90 0.044  63 3.0e+03  0.0e+00     3.8 0.93 0.120 2514  2714     1.5
4  0.51 0.85 0.048  51 1.6e+03 1.8e-308     3.0 0.95 0.098 1221  1383     1.7
5  0.38 0.71 0.061  40 6.0e+02 1.2e-100     2.4 0.96 0.066  275   402     2.0
6  0.38 0.68 0.076  30 3.0e+02  6.2e-46     2.2 0.96 0.053   56   151     2.1
7  0.34 0.58 0.101  21 1.5e+02  1.1e-21     2.0 0.97 0.044  -19    48     2.4
8  0.32 0.57 0.138  13 3.8e+01  3.1e-04     1.3 0.98 0.024  -67   -26     2.5
9  0.32 0.55 0.164   6 9.6e+00  1.4e-01     1.4 0.98 0.014  -39   -20     2.6
10 0.31 0.52 0.164   0 6.0e+00       NA     1.6 0.97    NA   NA    NA     2.7
11 0.29 0.53 0.240  -5 7.4e-02       NA     1.4 0.98    NA   NA    NA     2.7
12 0.29 0.48 0.412  -9 2.6e-06       NA     1.4 0.98    NA   NA    NA     2.6
13 0.30 0.52 0.719 -12 1.4e-08       NA     1.5 0.98    NA   NA    NA     2.7
14 0.29 0.52 1.000 -14 0.0e+00       NA     1.4 0.98    NA   NA    NA     2.7
15 0.36 0.68    NA -15 9.2e+02       NA     2.5 0.96    NA   NA    NA     2.2
    eChisq    SRMR  eCRMS eBIC
1  5.5e+03 9.0e-02 0.0969 4749
2  3.8e+03 7.4e-02 0.0875 3150
3  1.5e+03 4.8e-02 0.0614 1029
4  7.6e+02 3.3e-02 0.0480  347
5  2.0e+02 1.7e-02 0.0279 -122
6  1.2e+02 1.3e-02 0.0245 -126
7  6.4e+01 9.7e-03 0.0217 -106
8  1.0e+01 3.9e-03 0.0111  -95
9  2.8e+00 2.0e-03 0.0085  -46
10 2.5e+00 1.9e-03     NA   NA
11 1.1e-02 1.2e-04     NA   NA
12 1.3e-06 1.4e-06     NA   NA
13 5.4e-09 8.9e-08     NA   NA
14 1.4e-12 1.4e-09     NA   NA
15 2.3e+02 1.9e-02     NA   NA

In der Ergebnissdarstellung sehen wir verschiedene Metriken, anhand derer wir uns für die Anzahl der Faktoren entscheiden können. Wir schauen uns in diesem Beispiel insbesondere Very Simple Structure (VSS) und den maximalen durchschnittlichen Teilwert (MAP) an.

Durch VSS werden unter anderem drei Faktoren vorgeschlagen. Entsprechend schauen wir uns diese einmal kurz an, um uns ein Bild zu machen.

Im Anschluss daran betrachten wir das Ergebnis der minimalen durchschnittlichen Teilwerte (MAP), welche als die genauesten empirischen Schätzungen für die Anzahl der beizubehaltenden Faktoren betrachtet wird. Der MAP Wert schlägt uns einen Faktor vor, entsprechend gehen wir im folgenden von einem Faktor bzw. einer lateten Variable aus.

4.3 Rotation der Faktoren

Bei der Durchführung der Faktorenanalyse werden sogenannte Faktorladungen ermittelt, die anzeigen, wie stark jede Variable mit den extrahierten Faktoren zusammenhängt. Während des Analyseprozesses kann es vorkommen, dass die Faktorladungen rotiert werden, um eine eindeutigere und interpretierbarere Struktur der Faktoren zu erzielen. Die Rotation der Faktorladungen ermöglicht es, die Ausprägung der Faktoren auf weniger, aber stärker ausgeprägte Variablen zu konzentrieren, was die Interpretation und Verständlichkeit der Analyseergebnisse erleichtert. Es gibt verschiedene Rotationsmethoden, wie beispielsweise die Varimax- oder Quartimax-Rotation, die je nach Ziel der Faktorenanalyse angewendet werden können. Es existieren Dutzende von analytischen Rotationsmethoden, wobei Varimax die beliebteste orthogonale Rotationsmethode ist, während Promax und Oblimin die beliebtesten schrägen Rotationsmethoden sind. Sowohl bei Promax als auch bei Oblimin können wir den Grad der Korrelation zwischen den Faktoren kontrollieren (über die Parameter Kappa bzw. Delta).

Wichtig ist, dass sich die Interpretation der Faktorladungen zwischen orthogonalen und schrägen Rotationen unterscheiden. Bei orthogonalen Lösungen können die Faktorladungen als Korrelationen zwischen gemeinsamen Faktoren und gemessenen Variablen interpretiert werden. Diese Korrelationen reichen von -1,00 bis +1,00, und der Anteil der Varianz in einer gemessenen Variablen, der durch einen gemeinsamen Faktor beigetragen wurde, kann durch Quadrieren der Faktorladung berechnet werden. Im Gegensatz dazu ergeben sich bei schrägen Lösungen zwei verschiedene Arten von Faktorladungen: Struktur- und Musterkoeffizienten. Strukturkoeffizienten können auch als Korrelationen zwischen gemeinsamen Faktoren und den gemessenen Variablen interpretiert werden. Im Gegensatz dazu sind die Musterkoeffizienten keine einfachen Faktor-Variablen-Korrelationen mehr, sondern sie ähneln standardisierten partiellen Regressionskoeffizienten. Das heißt, sie sind Korrelationen zwischen gemeinsamen Faktoren und gemessenen Variablen, nachdem der Einfluss aller anderen gemeinsamen Faktoren kontrolliert (herausgerechnet) wurde. Dementsprechend können Musterkoeffizienten den Wert von 1,00 überschreiten und können nicht quadriert werden, um den Anteil der Varianz zu ermitteln, der eindeutig auf einen gemeinsamen Faktor zurückzuführen ist.

In unserem Fall greifen wir auf die etablierte Rotationsmethode varimax zurück, welches wir entsprechend im R-Code spezifizieren. Zusätzlich geben wir unsere erwartete Anzahl an Faktoren an, welche wir zuvor bestimmt haben (in unserem Fall: 3 und 1).

Wir starten mit der durch VSS vorgeschlagenen Anzahl von drei Faktoren.

fit3 =  principal(allbus_vertrauen, nfactors = 3, method = "ml", rotate = "varimax")
fit3

1: Mit der principal Funktion führen wir eine Faktorenanalyse durch. Hierfür wählen wir die Anzahl an Faktoren mit nfactors aus, legen ein Rotation mit rotate sowie eine Methode der Schätzung mittels method fest

Principal Components Analysis
Call: principal(r = allbus_vertrauen, nfactors = 3, rotate = "varimax", 
    method = "ml")
Standardized loadings (pattern matrix) based upon correlation matrix
                      RC1  RC3   RC2   h2   u2 com
Ver_Gesundheitswesen 0.65 0.14  0.11 0.45 0.55 1.2
Ver_BVerfG           0.69 0.34 -0.01 0.59 0.41 1.5
Ver_Bundestag        0.51 0.68  0.13 0.73 0.27 1.9
Ver_Verwaltung       0.51 0.36  0.24 0.45 0.55 2.3
Ver_kath_Kirche      0.09 0.15  0.90 0.85 0.15 1.1
Ver_evan_Kirche      0.18 0.18  0.88 0.83 0.17 1.2
Ver_Justiz           0.63 0.40  0.10 0.57 0.43 1.8
Ver_TV               0.60 0.28  0.13 0.46 0.54 1.5
Ver_Zeitung          0.64 0.30  0.13 0.52 0.48 1.5
Ver_Uni              0.68 0.23  0.01 0.51 0.49 1.2
Ver_Regierung        0.49 0.71  0.12 0.76 0.24 1.8
Ver_Polizei          0.69 0.16  0.17 0.53 0.47 1.2
Ver_Parteien         0.33 0.76  0.20 0.72 0.28 1.5
Ver_Kom_EU           0.25 0.89  0.14 0.88 0.12 1.2
Ver_EU_Par           0.26 0.89  0.14 0.88 0.12 1.2

                       RC1  RC3  RC2
SS loadings           4.04 3.85 1.84
Proportion Var        0.27 0.26 0.12
Cumulative Var        0.27 0.53 0.65
Proportion Explained  0.41 0.40 0.19
Cumulative Proportion 0.41 0.81 1.00

Mean item complexity =  1.5
Test of the hypothesis that 3 components are sufficient.

The root mean square of the residuals (RMSR) is  0.06 
 with the empirical chi square  2705.49  with prob <  0 

Fit based upon off diagonal values = 0.98

fit1 =  principal(allbus_vertrauen, nfactors = 1, method = "ml", rotate = "varimax")
fit1

1: Mit der principal Funktion führen wir eine Faktorenanalyse durch. Hierfür wählen wir die Anzahl an Faktoren mit nfactors aus, legen ein Rotation mit rotate sowie eine Methode der Schätzung mittels method fest

Principal Components Analysis
Call: principal(r = allbus_vertrauen, nfactors = 1, rotate = "varimax", 
    method = "ml")
Standardized loadings (pattern matrix) based upon correlation matrix
                      PC1   h2   u2 com
Ver_Gesundheitswesen 0.57 0.32 0.68   1
Ver_BVerfG           0.70 0.49 0.51   1
Ver_Bundestag        0.84 0.71 0.29   1
Ver_Verwaltung       0.66 0.43 0.57   1
Ver_kath_Kirche      0.41 0.17 0.83   1
Ver_evan_Kirche      0.48 0.23 0.77   1
Ver_Justiz           0.73 0.53 0.47   1
Ver_TV               0.64 0.41 0.59   1
Ver_Zeitung          0.68 0.46 0.54   1
Ver_Uni              0.62 0.39 0.61   1
Ver_Regierung        0.85 0.72 0.28   1
Ver_Polizei          0.63 0.39 0.61   1
Ver_Parteien         0.79 0.63 0.37   1
Ver_Kom_EU           0.81 0.66 0.34   1
Ver_EU_Par           0.81 0.66 0.34   1

                PC1
SS loadings    7.21
Proportion Var 0.48

Mean item complexity =  1
Test of the hypothesis that 1 component is sufficient.

The root mean square of the residuals (RMSR) is  0.09 
 with the empirical chi square  5969.7  with prob <  0 

Fit based upon off diagonal values = 0.96

4.4 Interpretation der Ergebnisse

Bei der Betrachtung des Outputs der Faktorenanalyse beginnen wir mit den Faktorladungen. Faktorladungen geben an, wie stark jede Variable mit den extrahierten Faktoren korreliert. Hohe positive Ladungen zeigen eine starke Beziehung zwischen der Variable und dem Faktor an, während hohe negative Ladungen darauf hindeuten, dass die Variable invers mit dem Faktor zusammenhängt. Variablen mit Ladungen nahe null haben wenig oder keine Beziehung zum jeweiligen Faktor. Durch die Betrachtung dieser Ladungen können wir die die Faktoren interpretieren und auch benennen. Auf diese Art und Weise können wir Rückschlüsse auf die zugrunde liegende latente Variable ziehen.

Wenn wir die Ergebnisse unserer ersten Faktorenanalyse - mit drei Faktoren - betrachten, sehen wir, dass die Faktorenladungen in den Spalten RC1 bis RC3 unterschiedlich stark ausgeprägt sind. Wenn wir die Indikatoren für die Spalte RC2 näher betrachten fällt uns auf, dass hier vor allem die beiden Indikatoren zu dem Vertrauen in die evangelische und katholische Kirche hohe Werte aufweisen, während alle anderen Faktorladungen niedriger ausfallen. Vor diesem Hintergrund können wir davon ausgehen, dass es sich bei dem Faktor RC2, um das Vertrauen in Kirchen handelt. Wir können dieses Vorgehen für die beiden anderen Faktoren wiederholen und auf diese Weise die Faktoren interpretieren.

Für den Fall der zweiten Faktorenanalyse - mit einem Faktor - übersteigen für alle Indikatoren die Faktorladungen über den Wert 0.3, was auf einen relativ starken und damit für uns guten Zusammenhang mit dem Faktor bzw. der latenten Variable spricht.

Welche der beiden Lösungen besser ist hängt von unserer theoretischen Grundlage und unserer Forschungsfrage ab. Entsprechend treffen wir an dieser Stelle keine pauschale Aussage, ob die eine oder andere Lösung grundsätzlich besser ist, sondern plädieren für eine reflektierte Auseinandersetzung und Abwägung zwischen den empirischen Ergebnissen und den theoretischen Annahmen.

Zusätzlich zur Interpretation der Faktorladungen ist es auch wichtig, die Uniquenes der Faktoren zu berücksichtigen. Diese zeigen an, wie viel Varianz in den Daten von jedem extrahierten Faktor erklärt wird. In anderen Worten sagt sie also aus, wie gut die Information der Variablen in den Faktoren insgesamt erhalten geblieben ist.

print(fit1$uniquenesses, digits = 2)

Ver_Gesundheitswesen           Ver_BVerfG        Ver_Bundestag 
                0.68                 0.51                 0.29 
      Ver_Verwaltung      Ver_kath_Kirche      Ver_evan_Kirche 
                0.57                 0.83                 0.77 
          Ver_Justiz               Ver_TV          Ver_Zeitung 
                0.47                 0.59                 0.54 
             Ver_Uni        Ver_Regierung          Ver_Polizei 
                0.61                 0.28                 0.61 
        Ver_Parteien           Ver_Kom_EU           Ver_EU_Par 
                0.37                 0.34                 0.34

Wenn wir auf die Uniqueness der einzelnen Indikatoren blicken, wird relativ schnell klar, dass wir eine Reihe von Indikatoren mit hohen Uniqueness-Werten haben, deren Varianz zu großen Teilen von der latenten Variable erklären wird und somit stärker als andere Indikatoren zu der latenten Variable “beitragen”.

Wie gebe ich die Ergebnisse korrekt an?

Die Ergebnisse von Regressionsanalysen werden meistens in einer Tabelle dargestellt. Für die Angabe im Text wird folgendes gebraucht:

✅ die Werte des Kaiser-Meyer-Olkin Kritierums (KMO)

✅ das Ergebnis des Barlett-Tests

✅ die Faktorladungen

✅ die Uniqueness

✅ die gewählte Rotations-Methode

Das Format ist normalerweise:

Beispiel: Zunächst wurde Faktorenanalyse der 15 gemessenen Indikatoren durchgeführt. Das Kaiser-Meyer-Olkin (KMO)-Maß für die Stichprobenadäquanz betrug 0,89. Dies deutet darauf hin, dass die Korrelationsmuster relativ kompakt sind und die Faktorenanalyse eindeutige und zuverlässige Faktoren ergeben sollte. Der Bartlett-Test auf Sphärizität war ebenfalls signifikant (χ2(105) = 33164.76, p < .001). Dies bedeutet, dass es einige Beziehungen zwischen den untersuchten Variablen gibt. Sowohl der KMO-Test als auch der Bartlett-Test bestätigen, dass die Faktorenanalyse angemessen ist.

Die Faktoren werden rotiert, um eine einfache Struktur zu erhalten. In diesem Fall wurde die varimax Rotationsmethode verwendet. Nach sorgfältiger Betrachtung der zusammenhängenden Variablen in der Analyse wurden dann die Faktorbezeichnung vorgeschlagen und in Tabelle 1 dargestellt. Dabei handelt es sich um Vertrauen in gesellschaftliche Institutionen. Für den Faktor wurden Faktorladungen erstellt (siehe Tabelle 1).

5 Danksagung und Literatur

Die Struktur und Inhalt dieser Seite orientiert sich an den folgenden Arbeiten. Ich möchte mich bei den Autor:innen sehr bedanken!

Daniela Keller Link
Field, A., Miles, J., & Field, Z. (2012). Discovering statistics using R. 749-811
Brown T. A. (2015). Confirmatory factor analysis for applied research (2nd ed.). New York, NY: Guilford Press. Watkins, M. W. (2018). Exploratory Factor Analysis: A Guide to Best Practice. Journal of Black Psychology, 44(3), 219–246. Link

Literatur und Beispiele aus der Praxis

Wir empfehlen euch folgende Lehrbücher, falls ihr weiterführende Informationen braucht.

📖 Field, Z., Miles, J., & Field, A. (2012). Discovering statistics using R. Discovering statistics using r, 1-992. Link

📖 Brown T. A. (2015). Confirmatory factor analysis for applied research (2nd ed.). New York, NY: Guilford Press. Watkins, M. W. (2018). Exploratory Factor Analysis: A Guide to Best Practice. Journal of Black Psychology, 44(3), 219–246. Link

📖 Fabrigar, L. R., & Wegener, D. T. (2012). Exploratory factor analysis. Oxford University Press.

Hier findet ihr ein Beispiel aus der Forschungspraxis:

🔬 Koirala, B. P., Araghi, Y., Kroesen, M., Ghorbani, A., Hakvoort, R. A., & Herder, P. M. (2018). Trust, awareness, and independence: Insights from a socio-psychological factor analysis of citizen knowledge and participation in community energy systems. Energy research & social science, 38, 33-40. Link