Häufigkeiten und deren Visualisierung

Zunächst ein paar Begriffserläuterungen: Bei der quantitativen Datenerhebung misst man die Ausprägung eines bestimmten Merkmals. Ein Merkmal kann zum Beispiel das Alter einer Person sein. Die Person ist dann der Merkmalsträger. Die Merkmalsausprägung bzw. der Messwert ist die konkrete Altersangabe, z.B. 23 Jahre. Die Menge aller Merkmalsträger, über die man durch die Untersuchung zu Erkenntnissen kommen will, heißt Grundgesamtheit. Oft kann man aber gar nicht oder nur sehr schwer die ganze Grundgesamtheit heranziehen und muss sich mit einer Teilmenge begnügen: Der Stichprobe. Die Daten sind erhoben, die Arbeitsumgebung ist eingerichtet, wir haben die Datensätze geladen und wissen, wie wir sie bearbeiten und visualisieren können. Nun wird es Zeit, sich einen ersten Eindruck von den statistischen Eigenschaften unserer Daten zu verschaffen. Von diesen Eigenschaften hängt ab, welche Methoden wir auf sie anwenden können und somit, welche Fragen wir mit ihnen überhaupt beantworten können. Dabei interessieren uns zunächst zwei Aspekte, erstens: Welche Methoden passen zur Beschaffenheit der Daten und zweitens: Welche inhaltlichen Eigenschaften können wir darauf aufbauend in den Daten erkennen? Ersteres ist abhängig vom Skalenniveau, für letzteres schauen wir uns einige der wichtigsten Maßzahlen (Parameter) an.
1 Häufigkeiten
Zur Beschreibung insbesondere nominaler Merkmale ist der Begriff der Häufigkeit wichtig.
Absolute Häufigkeit
Die absolute Häufigkeit gibt an, wie oft eine bestimmte Merkmalsausprägung im Datensatz vorkommt. Die absolute Häufigkeit kann folglich nur eine natürliche Zahl sein.
Relative Häufigkeit
Die relative Häufigkeit gibt den Anteil eines bestimmten Messwertes im Datensatz an. Sie berechnet sich, indem man die absolute Häufigkeit des jeweiligen Messwertes durch die Gesamtgröße des Datensatzes teilt. Die relativen Häufigkeiten summieren sich also zu 1 auf.
2 Maßzahlen
Wir werden hier, abhängig vom Skalenniveau, zwei verschiedene Arten von Maßzahlen betrachten. Das ist zum einen das Lagemaß, das uns etwas über die zentrale Tendenz der Daten sagt, also wo sich besonders viele Messwerte häufen bzw. wo der zentrale Punkt ist, um den sich die Messwerte gruppieren. Zum anderen schauen wir uns verschiedene Streuungsparameter an, mit deren Hilfe wir einschätzen können, wie stark unsere Messwerte vom Lageparameter abweichen.
2.1 Data Management
Im Folgenden werden wir aus dem Allbus-2021-Datensatz ein paar Beispiele herausgreifen, um die Berechnung und Visualisierung von Häufigkeiten und Parametern zu demonstrieren. Dazu installieren und laden wir zunächst die nötigen Pakete mit Hilfe von Pacman und dem p_load-Befehl:
Dann legen wir den Visualisierungshintergrund fest:
Nun laden wir den Allbus-Datensatz:
Bei den Häufigkeiten beschränken wir uns auf einen nominal skalierten Datensatz: Das Geschlecht (“sex”).
Anschließend konvertieren wir die Daten zu Zahlenwerten und entfernen fehlerhafte Daten:
allbus_messniveau_bsp = daten %>%
select("sex") %>%
na.omit() %>%
mutate(sex = haven::as_factor(sex))- 1
-
Wir erstellen ein neues Objekt basierend auf dem Datensatz
allbus_messniveau_bsp, - 2
-
Mit
selectwählen wir die Variablesexaus - 3
-
Wir entfernen mit der Funktion
na.omitfehlende Werte aus dem Datensatz - 4
-
Wir kodieren die Variable
sexals Faktor und übernehmen die Label.
3 Berechnung und Visualisierung von Häufigkeiten
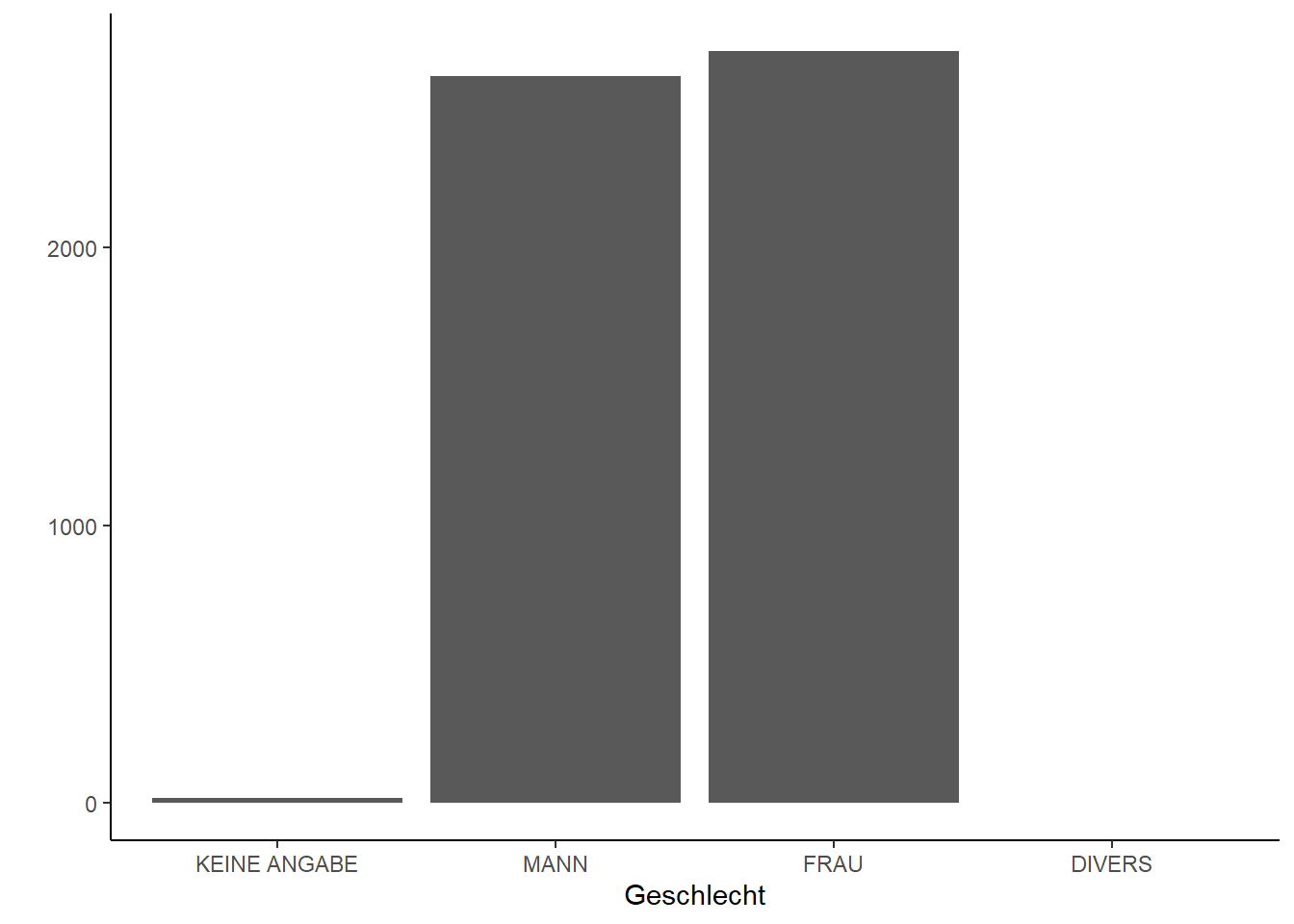
Die absoluten Häufigkeiten lassen sich einfach mit der table-Funktion abfragen. Im folgenden Codebeispiel schauen wir uns dazu die Häufigkeiten im Datensatz “sex” an. Uns werden zwei Zeilen ausgegeben: Die erste Zeile enthält den Tabellenkopf (1: männlich, 2: weiblich, 3: divers). Die zweite Zeile enthält zu jeder Merkmalsausprägung die zugehörige Anzahl (= absolute Häufigkeit):
geschlecht_haeufigkeit_abs = table(allbus_messniveau_bsp$sex)
stichprobengroesse = length(allbus_messniveau_bsp$sex)
geschlecht_haeufigkeit_abs- 1
- Ausgabe der Tabelle
KEINE ANGABE MANN FRAU DIVERS
20 2614 2705 3 Insgesamt summieren sie sich (wie erwartet) zu 5322 Merkmalsträgern auf, was auch der Größe des Datensatzes entspricht:
- 1
- Ausgabe der Summe der absoluten Häufigkeiten
- 2
- Ausgabe der Gesamtanzahl an Merkmalsträgern im Datensatz
[1] 5342
[1] 5342Die relativen Häufigkeiten können wir uns ausgeben lassen, indem wir den Inhalt der Tabelle durch die Gesamtanzahl der Merkmalsträger teilen:
geschlecht_haeufigkeit_rel = geschlecht_haeufigkeit_abs / stichprobengroesse
geschlecht_haeufigkeit_rel- 1
- Berechnung der relativen Häufigkeiten
- 2
- Ausgabe der Tabelle mit den relativen Häufigkeiten
KEINE ANGABE MANN FRAU DIVERS
0.0037439161 0.4893298390 0.5063646574 0.0005615874 Erwartungsgemäß summieren sich die relativen Häufigkeiten zu 1 auf:
Eine Möglichkeit der Darstellung von Häufigkeiten ist das Balkendiagramm:
Auf den ersten Blick lässt sich so ein generelles Bild des Datensatzes machen: Es sind in etwa so viele Männer wie Frauen im Datensatz, wobei Frauen etwas stärker vertreten sind. Personen, die sich weder als Mann noch als Frau identifizieren, kommen nur in sehr geringer Zahl vor (3 Fälle, die leider nicht korrekt angezeigt werden).